This is my attempt to explore the SIMD paradigm. I come at it as someone who has worked with other parallelization models- threads, distributed systems and GPUs, SIMD has been my one blind spot. For a while I was okay with that. My tech diet hasn’t been very kind to SIMD, AVX-512 in particular. There were reports about CPU heating and downclocking (probably not true anymore), and when the hardware did seem to work as promised, taking advantage of it from software wasn’t straightforward (this one is probably still true).

My goal here is two-fold: 1) Performance: How much scaling we can actually get from all these extra lanes with reasonable development effort. Ideally, it should be 16x for single-precision. 2) Programmability: Contrasting SIMD way of thinking about parallel programs with SIMT (Single Instruction Multiple Threads), specifically CUDA. (SPMD is probably a better term, but I’ll stick with SIMT here)

Benchmark Problem

Finding a good problem for this is actually not that trivial. The number of problems that 1) can be meaningfully accelerated by SIMD and 2) quickly be explained for a blogpost is not very large. The issue is memory, which is often the bottleneck for interesting problems, but ideal SIMD speedup can only come from problems that are compute bound.

Here’s arguably the most well-known example people use to introduce SIMD, including an interestingly titled talk from CppNow that I recently found- “How to Leverage SIMD Intrinsics for Massive Slowdowns”:

void axpy_scalar(const float *a, const float *x, const float *b, float *out std::size_t n) {
    for (std::size_t i = 0; i < n; ++i) {
        out[i] = a[i] * x[i] + b[i];
    }
}

The video talks about how explicit vectorization using intrinsics can lead to a slowdown compared to auto vectorization, due to things like loop unrolling, ILP etc. The problem is, it’s just a bad, bad example to talk about SIMD at all, regardless of whether it’s explicit or auto-vectorized. Take a guess: if we completely disable vectorization here (i.e. force the compiler to use purely scalar code), how much of a slowdown will we see vs a good vectorized code on a 16-lane wide SIMD? 16x? 8x? 8%?

The answer, if it’s not obvious from my tone already:), is 8%. Here’s a (very) simplistic explanation why: for the time it takes to feed 16 bytes of data to CPU in above code (to process 1 element), it can execute 32 compute ops. But we only have 2 ops here. So the ALUs are already sitting idle most of the time even in the scalar code, SIMD is trying optimizing something that doesn’t really matter.

My testcase of choice here is K-Means algorithm- an unsupervised clustering algorithm. It’s a pretty simple algorithm- a Numpy version shouldn’t take more than 15-20 lines.

centroids = sample K points from dataset (K=8 throughout this post)

while centroids are not converged:
    for each sample in dataset:   // compute_labels()
        assign it to a cluster with "closest" centroid

    for each cluster:             // compute_centroids()
        choose a better centroid by averaging each sample

The dataset samples in this case is going to be pixels of an image, so K-Means will basically do image segmentation based on pixel values. This K-Means variant should be a pretty good algorithm to try the SIMD paradigm out. We have lots of computations relative to data movement (aka high arithmetic intensity). Memory access is predictable and linear. The two functions above exhibit two different parallel programming patterns, which will come in handy in evaluating the programmability aspects.

Original Image
Segmentation with 8 clusters

Baseline(s)

We have two baselines here: the pure scalar version and auto-vectorized code produced by two compilers: GCC 14.2 and Intel’s ICPX 2024.2. The scalar code should give us an idea of how much AVX-512 actually scales (ideally 16x for single-precision data), and the auto-vectorized version will tell us if the considerable pain of writing intrinsics was really worth the trouble.

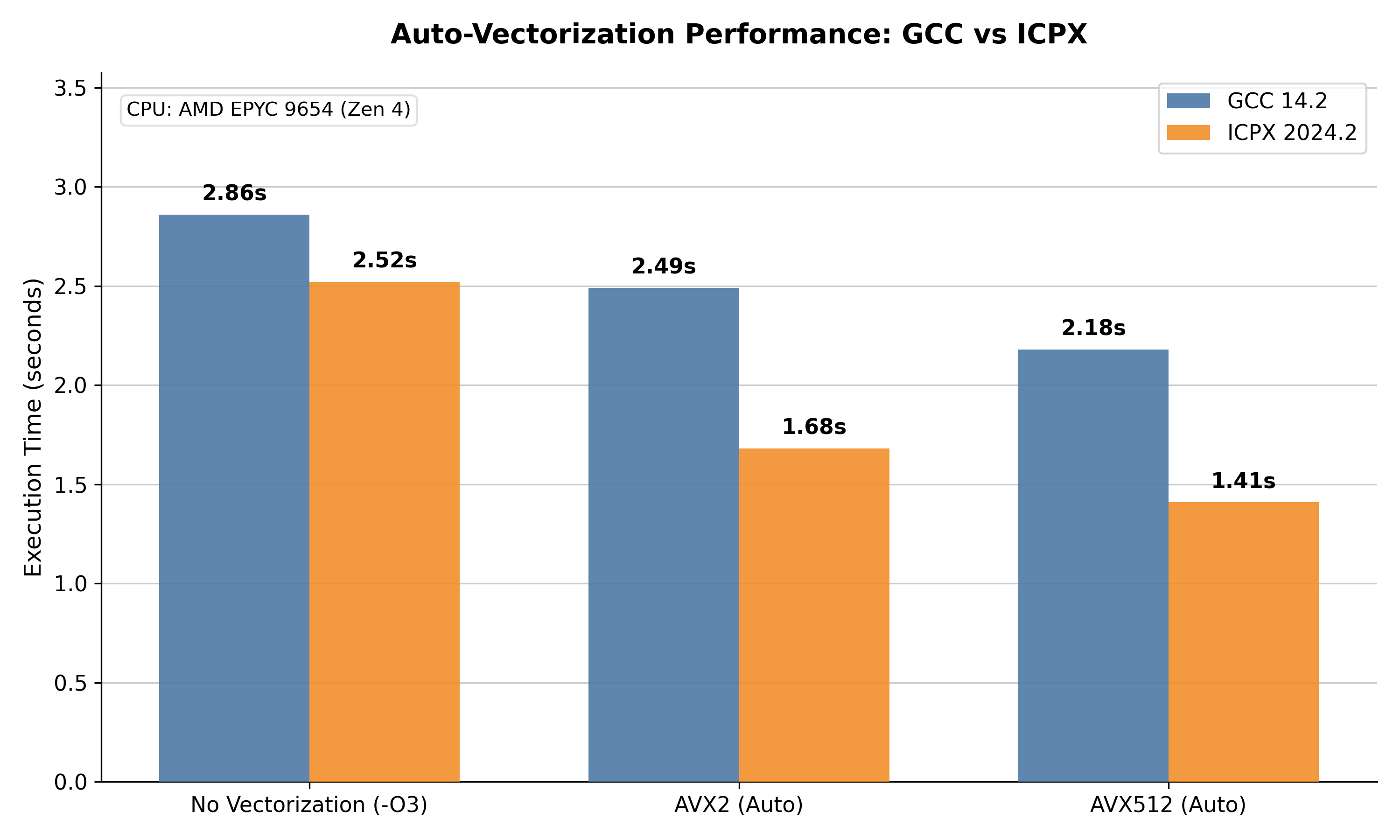
The results are pretty interesting. We see clear improvement with both AVX2 and AVX512 variants from both compilers, but nowhere close to the 8x or 16x ideal scaling.

Let’s look at these runtimes from another angle by doing a quick speed-of-light analysis. Having a single, obvious bottleneck (compute in this case) makes our life a lot easier. The theoretical max for the CPU here (AMD EPYC 9654) in single-precision is 3.7 GHZ: i.e. 3.7 GFlops/sec. With AVX-512, we have 16 32-bit ops/cycle, so 16*3.7=59.2 GFlops/sec. As for actual computations, our image have about 5 million pixels, we fix K-means iteration number to 20, and in each iteration with 8 centroids, a pixel requires roughly 200 flops. So we have total 5 million * 200 * 20 = 20 GFlops of computation. Ideally, the program should take about 20/59.2= 337ms. The best compilers can do here is 1.4 seconds, a 4.2x slowdown.

There are quite a few nuances in this calculation (e.g. we’re ignoring FMA, using boosted speed etc). But this doesn’t change the overall picture: we have a program that should be highly SIMD-iable, and auto-vectorization won’t take us there. On to the world of intrinsics we go.

AVX-512

Our K-means have two main functions. The first one, compute_labels, finds the closest centroid for each pixel. This is an example of “embarrassingly parallel” pattern, meaning what we do for each pixel is fully independent of what’s going on in other pixels. Below is a snippet from the function:

Scalar/CUDA SIMD (AVX-512) 
float dx_norm = static_cast<float>(dx) * inv_width;
float dy_norm = static_cast<float>(dy) * inv_height;
float spatial_norm = (dx_norm*dx_norm + dy_norm*dy_norm)
spatial_norm /= 2.0f;

const float weight = 0.85f;
float dist = weight * color_norm 
dist += (1.0f - weight) * spatial_norm;

if(dist < best_dist){      
    best_dist = dist;      
    best_k = k;            
}
out_labels[i] = best_k;

__m512 dx_normv = _mm512_mul_ps(_mm512_cvtepi32_ps(dxv), _mm512_set1_ps(inv_width));
__m512 dy_normv = _mm512_mul_ps(_mm512_cvtepi32_ps(dyv), _mm512_set1_ps(inv_height));

dx_normv = _mm512_mul_ps(dx_normv, dx_normv);
__m512 spatial_normv = _mm512_fmadd_ps(dy_normv, dy_normv, dx_normv);
spatial_normv = _mm512_mul_ps(spatial_normv, _mm512_set1_ps(0.5));
                
spatial_normv = _mm512_mul_ps(spatial_normv, _mm512_set1_ps(1-weight));
__m512 distv = _mm512_fmadd_ps(color_normv, color_norm_weight, spatial_normv);

__mmask16 mask = _mm512_cmplt_ps_mask(distv, best_dist);
best_dist = _mm512_mask_mov_ps(best_dist, mask, distv);  
best_k = _mm512_mask_mov_epi32(best_k, mask, _mm512_set1_epi32(k));

_mm512_storeu_si512(out_ptr, best_k);

SIMD intrinsics doesn’t really leave a good first impression, does it?

Interestingly, CUDA (an example of SIMT) would look pretty much the same as scalar code in this case. For those who don’t know, SIMT exposes a more “scalar”-like interface. In this case, your code would define the work for just a single pixel, and hardware/compiler together does the job of parallelizing the for loop.

I don’t want to anthropomorphize, but SIMD looks “objectively” ugly compared to CUDA/regular CPP code, and this is after ignoring certain real-world issues like complication from supporting different archs, extra loop for holdovers etc. But it’s not just looks. GCC fails to auto-vectorize the scalar version because of that simple if condition in the snippet, whereas CUDA gracefully handles this. However you look at it, CUDA wins for this function hands down.

But before we move on, it’s worth asking how exactly CUDA abstracts away these verbose SIMD code, because behind the scene, it’s using pretty similar SIMD-like hardware. The if here is implemented by the warp scheduler, which implements the masking necessary to turn off threads that don’t take a branch. And there’s a lot going on behind the simple store operation in the end: out_labels[i] = best_k; (or any load). These two abstractions lead to two of the most well-known performance bugs in CUDA code: Warp divergence and Uncoalesced memory access. For example, if the data here wasn’t laid out so neatly in the memory, maybe because we have Array-of-(large) structs layout or data is truly random access, both CUDA warp and SIMD store operations will have to resort to basically a for loop. SIMD makes that explicit, CUDA hides it from the developers. This can have a dramatic performance impact, more on GPU than CPU.

I should also note while the SIMD code is bit too verbose for my taste, once the hard part, architecture and data-structure is done, I didn’t feel like writing it was more difficult than writing scalar code. It requires a bit more typing (or lots more googling), sure, but not necessarily more thinking.

The second function, compute_centroids is more interesting. This gathers all the pixels that has been assigned a similar label, and compute a new centroid (and color) for this group. Here’s what the main loop looks like:

Scalar/CUDA (Pseudocode) SIMD (Pseudocode) 
for(int h=0; h<height; h++){
    for(int w=0; w<width; w++){
        int i = h*width+w;
        int k = cluster[i];
        sum_r[k] += R[i]; 
        count[k]++;       
    }
}


for(int h=0; h<height; h++){
    for(int w=0; w<width; w+=L){     
        iv = [0..15] + h*width+w     
        __m512i kv = cluster[iv];    
        sum_r[kv] += R[iv];  // CONFLICT!        
        count[kv] += 1;      // CONFLICT!         
    }
}

Note that unlike the last code, there is potential conflict between SIMT threads (or SIMD lanes) here, since all pixels with a similar label are incrementing a single centroid data. This is an important detail.

For both CUDA and SIMD, we can take an easy route here: atomicAdd with CUDA and a serial for loop over SIMD length with AVX-512. The performant route with AVX-512 would probably include the instruction vpconflictd, but I couldn’t really find any elegant way to use it. Documentation and code samples were surprisingly sparse for such a common pattern. After spending some time optimizing this, I ended up with a version that has a for loop over the centroids, along with masks and reduction instruction. Not elegant, but seems to work pretty well.

In contrast, CUDA allows us to progressively optimize this code by gradually adding more complexity, for example by doing warp level and block level synchronizations first before writing to device memory. This is the positive. The downside is that each of this optimization forces us to move out of the warm comfort of SIMT abstraction and reckon with one more GPU hardware implementation detail. The final optimized CUDA code would look very, very different from this scalar version. Overall, getting close to hardware limit felt much easier with SIMD than CUDA. Official docs from Nvidia recommends developers to use their libraries instead of hand-rolling these primitives.

Anyway, how does our final performance look with intrinsics?

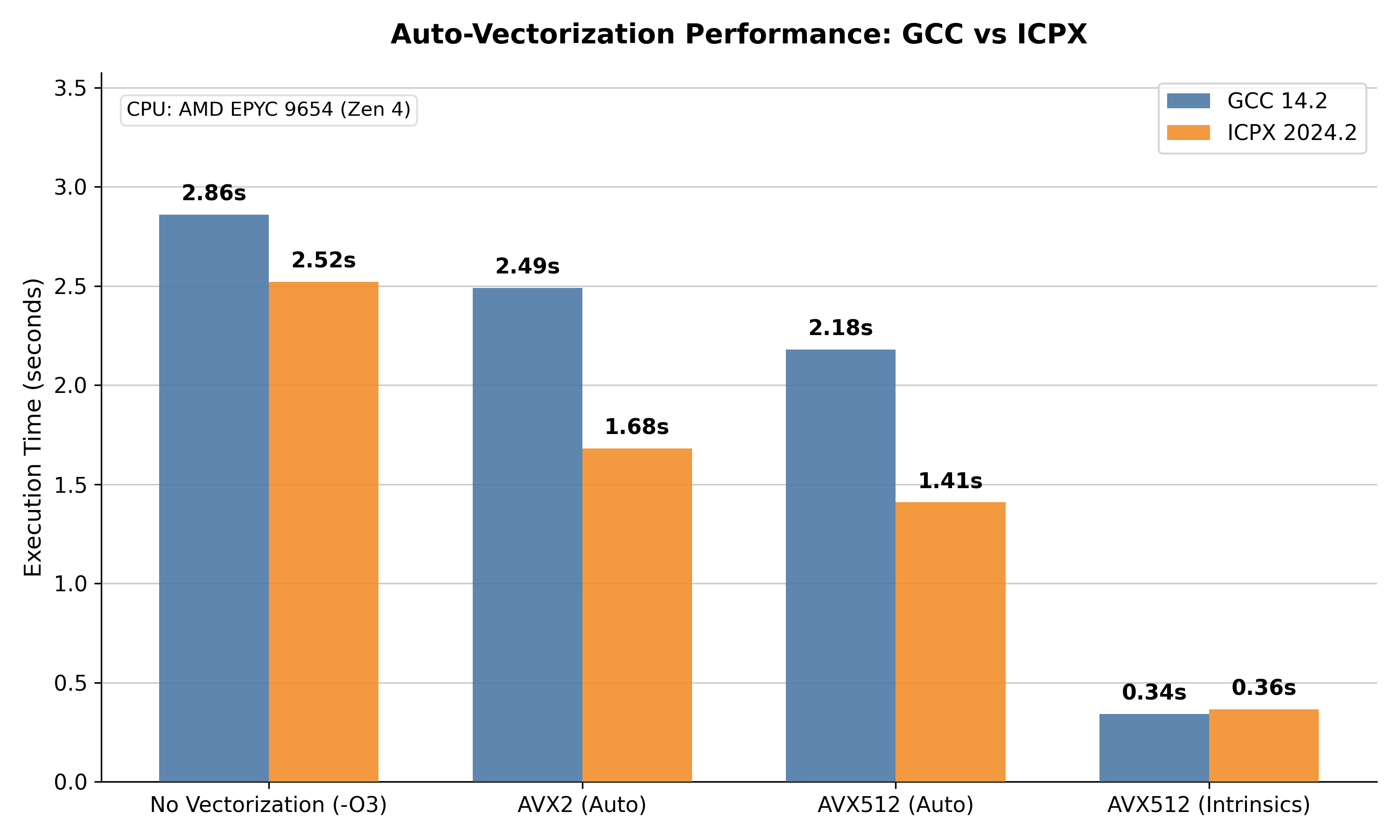
Not bad! This is 7-8.5x better compared to scalar code- around half of the ideal scaling, but closer to what people observe for SIMD-friendly code in practice. This is also 4x faster than best auto-vectorized codes. Interestingly, the final runtime (344ms) is surprisingly close to the rough speed-of-light estimate we had before. That doesn’t mean we’re at 98% of theoretical upper bound, that estimate was pretty rough. But I’ve been doing this sort of analysis before starting CUDA development, and I have never gotten this close to the upper limit, either for real or toy exercises.

Auto-vectorization did lot worse than I anticipated (4x), so I dug a little deeper. The main difference came from the first compute_labels function. Here’s what the key loops look like


for(int h=0; h<height; h++)}
    for(int w=0; w<width; w++){
        int best_k = 0;
        float best_dist = 999999999.0;
        for(int k=0; k<K; k++){
            ...
            if(dist < best_dist){
                best_dist = dist;
                best_k = k;
            }
    ...

GCC got tripped up by the presence of the if the conditional, the generated assembly was fully scalar. ICPX did vectorize, hence the ~40% better runtime. But the real issue is that both tried to vectorize the inner loop over centroids, not over the pixels. We know this is not a great idea since number of centroids will be lot lower than number of pixels, but there’s no easy way to encode that info in regular C++.

Final Thoughts

I’m concluding this exercise with pretty positive impressions for AVX-512, both in programmability and performance. I was expecting it to throw up some roadblocks and it didn’t. I have seen it argued that SIMD failed to get good adoption partly because it lacked a good programming model. At least for this admittedly simple exercise, I don’t really see how moving from this explicit SIMD-type code to an ISPC or CUDA like SIMT model would be beneficial. In fact, for more complicated code, I believe reasoning about performance would get more complicated with those abstractions compared to low-level SIMD.

I can’t comment on ISPC because I don’t know it. But I do know CUDA, it has many virtues, but simplicity is not of them. CUDA architects never had a dogmatic loyalty to the elegance of the SIMT model, they happily exposed every ugly details of underlying hardware to the programmer if that allows a bit more performance. Writing any good CUDA program requires looking at it from the thread, warp, thread block- every level of this deep hierarchy. I think it’s interesting that two of the most widely used DSLs that AI community uses to program GPUs, Triton and Cutlass, has a “Tile-based” model that is much closer in spirit to the explicit SIMD than SIMT.

In CPU world there is a desire to shield programmers from those low-level details, but I think there are two interesting forces at play now-a-days that’ll change it soon. On one hand, Dennard Scaling (aka free lunch) is long gone, hardware landscape is getting increasingly fragmented and specialized out of necessity, software abstractions are getting leakier, forcing developers to be aware of the lowest levels of abstraction, hardware, for good performance. On the flip side, thanks to LLMs, actual generation of code is becoming almost zero-cost, pushing developer responsibility to higher levels of abstractions like architecture and design. I think explicit SIMD is pretty perfect for this era- low-level enough to fully utilize the hardware but high level enough to exploit many compiler optimizations (and for human review). This creates a possible workflow where we developers architect our program in a hardware-friendly way (e.g. SoA memory layout instead of AoS), write the hot loops in scalar version, and hand off the task of porting to explicit SIMD to LLMs, optionally with some domain knowledge (“Parallelize over pixel loops since K is small”). With the latest batch of LLM models, I believe this is doable for a “real-world” program, but I’ll leave that for a future post (For now, see Appendix 2).

Appendix

[1] see Matt Pharr’s famous The story of ispc series.)

[2] https://parallelprogrammer.substack.com/p/why-we-need-simd-the-real-reason

[3] https://lemire.me/blog/2025/08/09/why-do-we-even-need-simd-instructions/

[4] https://lemire.me/blog/2025/02/14/avx-512-gotcha-avoid-compressing-words-to-memory-with-amd-zen-4-processors/

[5] https://www.youtube.com/watch?v=GleC3SZ8gjU

Appendix 2: LLMs

So far, I’ve used LLM for mainly 3 purposes:

  1. Look-up right AVX-512 instructions. (e.g. “AVX512 instruction to reduce fp32 with mask?”) The official intel doc isn’t beginner friendly at all.
  2. Create the performance plots.
  3. Look at all dumped assembly and highlight regions of interest.

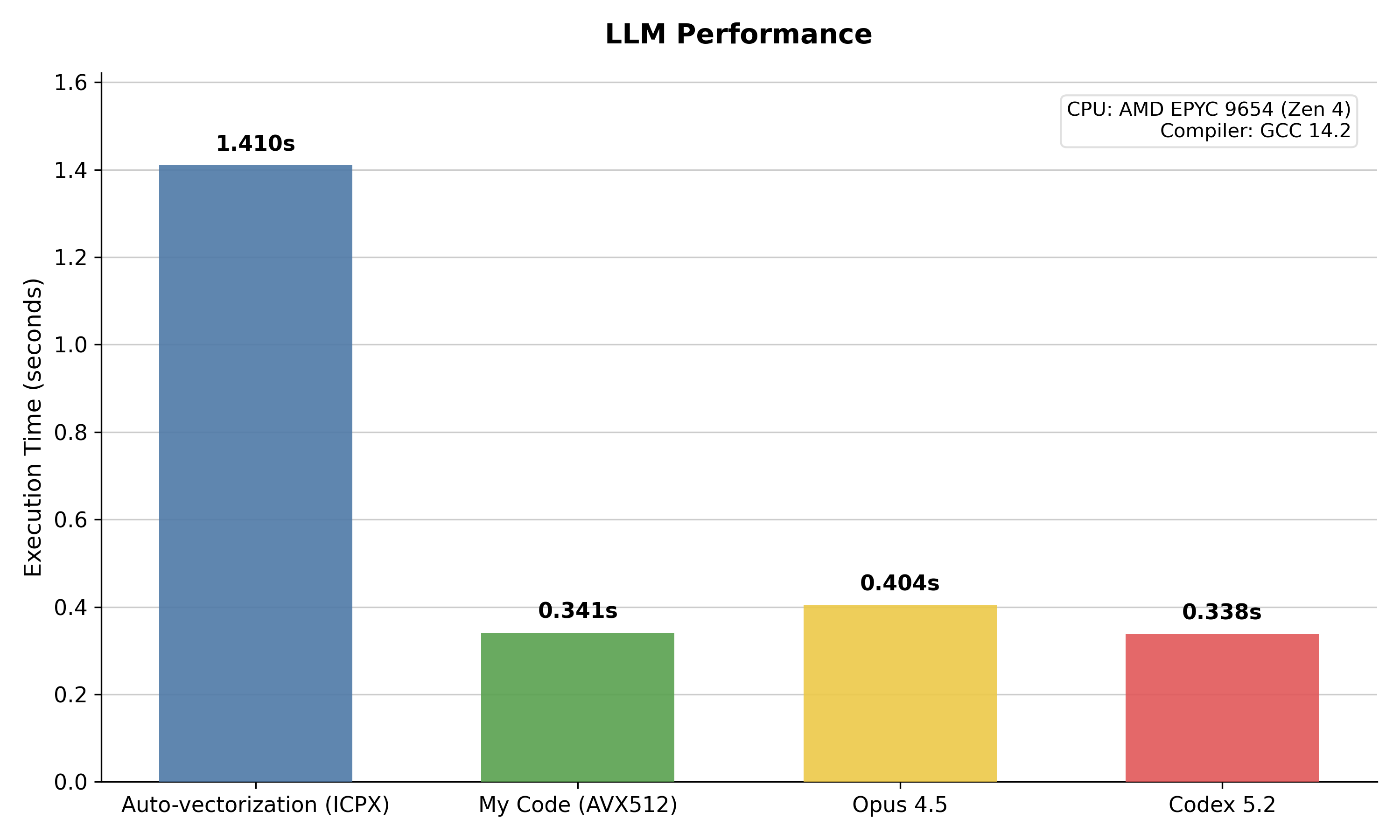
Here, I tried porting the scalar code to explicit AVX-512 using Codex 5.2 and Opus 4.5. A single prompt was used to port both functions at once: “Port compute_labels() and compute_centroids() functions here to AVX-512 using intrinsics. Parallelize the loop over pixel width at compute_labels(), assume width will be divisible by 16. No of centroids (K) will be low (<20). Order of floating point ops doesn’t matter”.

I truly one-shotted this, didn’t have to play around with prompt, didn’t need to do any further prompt. No context was supplied except the scalar code. Both models generated correct code at first try. And here’s the performance result: